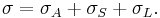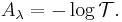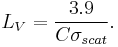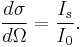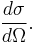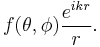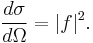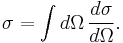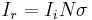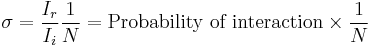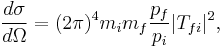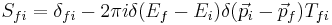Scattering cross-section

The scattering cross-section, σ_scat, is a hypothetical area which describes the likelihood of light (or other radiation) being scattered by a particle. In general, the scattering cross-section is different from the geometrical cross-section of a particle, and it depends upon the wavelength of light and the permittivity, shape and size of the particle. The total amount of scattering in a sparse medium is determined by the product of the scattering cross-section and the number of particles present. In terms of area, the total cross-section (σ) is the sum of the cross-sections due to absorption, scattering and luminescence

$\sigma = \sigma_A %2B \sigma_S %2B \sigma_L.\$

The total cross-section is related to the absorbance of the light intensity through Beer-Lambert's law, which says absorbance is proportional to concentration: 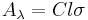$A_\lambda = C l \sigma$ , where C is the concentration as a number density, A_λ is the absorbance at a given wavelength, λ, and l is the path length. The extinction or absorbance of the radiation is the logarithm (decadic or, more usually, natural) of the reciprocal of the transmittance:^[1]

$A_\lambda = - \log \mathcal{T}.\$

1 Relation to physical size
2 Meteorological range
3 Units
4 Classical Mechanics
5 Quantum Mechanics
- 5.1 Relation to the S matrix
6 See also
7 References

Relation to physical size

There is no simple relationship between the scattering cross-section and the physical size of the particles, as the scattering cross-section depends on the wavelength of radiation used. This can be seen when driving in foggy weather: the droplets of water (which form the fog) scatter red light less than they scatter the shorter wavelengths present in white light, and the red rear fog light can be distinguished more clearly than the white headlights of an approaching vehicle. That is to say that the scattering cross-section of the water droplets is smaller for red light than for light of shorter wavelengths, even though the physical size of the particles is the same.

Meteorological range

The scattering cross-section is related to the meteorological range, L_V:

$L_V = \frac{3.9}{C \sigma_{scat}}.\$

The quantity Cσ_scat is sometimes denoted b_scat, the scattering coefficient per unit length.^[2]

Units

Its SI unit is the square meter, m², although smaller units are usually used in practice. The name cross-section arises because it has the dimensions of area.

When the scattered radiation is visible light, it is conventional to measure the path length in centimetres. To avoid the need for conversion factors, the scattering cross-section is expressed in cm² (1 cm² = 10⁻⁴ m²) and the number concentration in cm⁻³ (1 cm⁻³ = 10⁻⁶ m⁻³). The measurement of the scattering of visible light is known as nephelometry, and is effective for particles of 2–50 µm in diameter: as such, it is widely used in meteorology and in the measurement of atmospheric pollution.

Scattering cross-sections are also widely used in the description of the scattering of neutrons by atomic nuclei. In this case, the conventional unit is the barn, b, where 1 b = 10⁻²⁸ m² = 100 fm².^[3]

The scattering of X-rays can also be described in terms of scattering cross-sections, in which case the square ångström, Å², is a convenient unit: 1 Å² = 10⁻²⁰ m² = 10⁴ pm².

Classical Mechanics

In classical mechanics, the differential cross section is defined as follows: let a beam of intensity 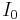$I_0$ (measured in number of particles per area per time) be incident on a scattering center. In general, the angle at which a particle is scattered is a function of impact parameter. The number of scattered particles per solid angle per time, 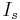$I_s$ is therefore well defined. We define the differential cross section to be

${d \sigma \over d \Omega} = \frac{I_s}{I_0}.$

Note that this quantity has units of area. Furthermore, it depends only on the geometry of the scattering center, and not on the incident flux or distance of the detector from the scattering center. The geometric interpretation is as follows: consider particles that scatter through a solid angle 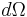$d \Omega$ and ask what values of impact parameter produced them. These impact parameters form a differential area, 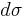$d \sigma$ in space. The differential cross section is simply

${d \sigma \over d \Omega}.$

Quantum Mechanics

In quantum mechanics, the wave function of the incident particle is a plane-wave with amplitude 1, that is, 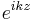$e^{ikz}$ . In general the scattered wave is of the form

$f(\theta,\phi) \frac{e^{i k r} }{r}.$

We then have as the definition of differential cross section

${d \sigma \over d \Omega} = |f|^2.$

This has the simple interpretation of the probability of finding a scattered particle within a given solid angle.

The integral cross section is the integral of the differential cross section on the whole sphere of observation (4 $\pi$ steradian):

$\sigma=\int d\Omega \, {d \sigma \over d \Omega}.$

A cross section is therefore a measure of the effective surface area seen by the impinging particles, and as such is expressed in units of area. Usual units are the cm², the barn (1 b = 10⁻²⁸ m²) and the corresponding submultiples: the millibarn (1 mb = 10⁻³ b), the microbarn (1 $\mu$ b = 10⁻⁶ b), the nanobarn ( 1 nb = 10⁻⁹ b), the picobarn (1 pb = 10⁻¹² b), and the shed (1 shed = 10⁻²⁴ b). The cross section of two particles (i.e. observed when the two particles are colliding with each other) is a measure of the interaction event between the two particles. 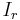The cross section is proportional to the probability that an interaction will occur; for example in a simple scattering experiment the number of particles scattered per unit of time (current of scattered particles $I_r$ ) depends only on the number of incident particles per unit of time (current of incident particles 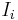$I_i$ ), the characteristics of target (for example the number of particles per unit of surface N), and the type of interaction. For 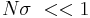$N\sigma\ << 1$ we have

$I_r=I_iN\sigma\,$

$\sigma={{I_r}\over{I_i}}{{1}\over{N}}={\hbox{Probability of interaction}}\times{{1}\over{N}}$

Relation to the S matrix

If the reduced masses and momenta of the colliding system are m_i, 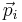$\vec{p}_i$ and m_f, 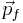$\vec{p}_f$ before and after the collision respectively, the differential cross section is given by

${d\sigma \over d\Omega} = (2\pi)^4 m_i m_f {p_f \over p_i} |T_{fi}|^2,$

where the on-shell T matrix is defined by

$S_{fi} = \delta_{fi} - 2\pi i \delta(E_f -E_i) \delta(\vec{p}_i-\vec{p}_f) T_{fi}$

in terms of the S matrix. The 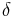$\delta$ function is the distribution called the Dirac delta function. The computation of the S matrix is the main aim of the scattering theory.

References

^ Bajpai, P.K.. "2. Spectrophotometry". Biological Instrumentation and Biology. ISBN 8121926335. http://books.google.com/?id=THq-cOPO8RQC&pg=PA14&dq=%22extinction+coefficient%22+transmittance+length+concentration.
^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Scattering cross-section, σ_scat".
^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (8th ed.), pp. 127–28, ISBN 92-822-2213-6, http://www.bipm.org/utils/common/pdf/si_brochure_8_en.pdf